Understanding Matrices and Vectors: Essential Linear Algebra Concepts for Data Science
ML (Part 10)
📚Chapter: 3 -Linear Algebra
If you want to read more articles about Machine Learning n, don’t forget to stay tuned :) click here.
Understanding Matrices and Vectors in Linear Algebra
Let’s get started with our linear algebra review. In this tutorial, I want to tell you what are matrices and what are vectors.
Sections
Introduction
How Machine Learning Uses Linear Algebra to Solve Data Problems
Linear Algebra Operations
What is meant by matrix
matrix example
Dimension of the matrix
How to refer to specific elements of the matrix
Vectors
How to refer to specific elements of the Vector
Types of Vectors
Matrix in Python
Section 1- Introduction
Machine learning is a rapidly growing field that relies heavily on mathematical concepts and tools. Matrices and vectors, in particular, play a crucial role in various aspects of machine learning algorithms. In this blog post, we will explore the significance of matrices and vectors in machine learning and discuss how they are used to represent and manipulate data, as well as optimize models.
Linear algebra is a fundamental branch of mathematics that deals with vector spaces and linear transformations. Matrices and vectors are two key concepts in linear algebra that form the foundation for solving systems of linear equations, performing transformations, and understanding higher-dimensional spaces. In this blog post, we will delve into the world of matrices and vectors, exploring their properties, operations, and applications.
Section 2- How Machine Learning Uses Linear Algebra to Solve Data Problems
Machines or computers only understand numbers. These numbers need to be represented and processed in a way that lets machines solve problems by learning from the data instead of learning from predefined instructions (as in the case of programming).All types of programming use mathematics at some level. Machine learning involves programming data to learn the function that best describes the data. The problem (or process) of finding the best parameters of a function using data is called model training in ML. Therefore, in a nutshell, machine learning is programming to optimize for the best possible solution — and we need math to understand how that problem is solved. The first step towards learning Math for ML is to learn linear algebra. Linear Algebra is the mathematical foundation that solves the problem of representing data as well as computations in machine learning models. It is the math of arrays — technically referred to as vectors, matrices, and tensors.
Linear Algebra is the backbone of Machine Learning model algorithm in Data science.
It contributes in the process in data science, such as
Linear Algebra in Data Representation
Linear Algebra in Data Preprocessing
Linear Algebra in Dimensionality Reduction
Linear Algebra in Feature Engineering
Linear Algebra in Machine Learning Algorithm
Linear Algebra in Recommendation Systems
Linear Algebra in Model Interpretation
1. Representation of Data
One of the fundamental applications of matrices and vectors in machine learning is the representation of data. In most machine learning tasks, data is typically organized in a tabular format, where each row represents an observation and each column represents a feature or attribute. This tabular structure can be represented as a matrix, where each element corresponds to a specific value in the dataset.
The fuel of ML models, that is data, needs to be converted into arrays before you can feed it into your models. The computations performed on these arrays include operations like matrix multiplication (dot product). This further returns the output that is also represented as a transformed matrix/tensor of numbers.
For example, consider a dataset of housing prices with features such as the number of bedrooms, square footage, and location. This dataset can be represented as an m x n matrix, where m is the number of observations (rows) and n is the number of features (columns). Each element in the matrix represents the value of a specific feature for a particular observation.
Linear algebra basically deals with vectors and matrices (different shapes of arrays) and operations on these arrays. In NumPy, vectors are basically a 1-dimensional array of numbers but geometrically, they have both magnitude and direction.Our data can be represented using a vector. In the figure below, one row in this data is represented by a feature vector which has 3 elements or components representing 3 different dimensions. N-entries in a vector makes it n-dimensional vector space and in this case, we can see 3-dimensions.
In the context of data science, particularly in machine learning, the significance of linear algebra becomes evident when dealing with datasets that have numerous features, making visualization and manual judgment challenging. While we can easily visualize and draw lines in 2 or 3-dimensional Cartesian space, real-world datasets often involve a high-dimensional space (N-dimensions) that is impractical to visualize. This is where the power of linear algebra comes into play. It allows us to apply mathematical principles to machine learning models, enabling the creation of decision boundaries or planes in N-dimensional space for accurate data classification and analysis.
Data representation includes transforming data into vectors and matrices, which are structured mathematical objects that can be manipulated to perform operations like addition, multiplication, and transformation.
2. Linear Algebra in Data Preprocessing
Data preprocessing in the context of linear algebra involves various techniques and operations applied to raw data to make it suitable for analysis, modeling, or other mathematical operations using linear algebra. Data Scaling, Normalization, Standardization, Robust Scaling
3- Linear Algebra in Dimensionality Reduction
Linear algebra plays a fundamental role in dimensional reduction techniques, which are used to reduce the number of features (dimensions) in a dataset while preserving as much relevant information as possible. Linear algebra techniques like PCA and eigen decomposition are commonly used in these methods. Eigenvalue, Eigenvector, Principal Component Analysis (PCA), Singular Value Decomposition (SVD)
4. Linear Algebra in Feature Engineering
Linear algebra plays a significant role in feature engineering, which is the process of creating new features or transforming existing ones to improve the performance of machine learning models. Feature Transformation, Feature Cross-Products,Feature Selection-Encoding Categorical Variables
5. Linear Algebra in Machine Learning Algorithm
In Mathematics, particularly linear algebra, forms the foundation of many machine learning algorithms. Euclidean Distance, Manhattan Distance, Unit Vector, Distance From point to plane, Kernel function.
6. Linear Algebra in Recommendation System
Linear algebra plays a fundamental role in recommendation systems, which are algorithms designed to suggest items (e.g., products, movies, music, articles) to users based on their preferences and behavior.for example,Matrix Factorization,User-Item Interaction Matrix,Content-Based Filtering,Collaborative Filtering,Cosine Similarity
7. Linear Algebra in Model Interpretation
Model interpretation using linear algebra involves a detailed analysis of a machine learning model’s coefficients, relationships between variables, and the impact of individual features on model predictions.for example Coefficient Interpretation, Orthogonalization, Residual Analysis-, Feature Importance
Section 3. Linear Algebra Operations
Matrices and vectors provide a powerful framework for performing various linear algebra operations, which are essential in many machine learning algorithms. These operations include addition, subtraction, multiplication, and division.
For instance, matrix addition allows us to combine datasets or add up the values of corresponding elements. Matrix multiplication enables us to perform transformations on data or calculate the dot product between two vectors. These operations are often utilized in tasks such as dimensionality reduction, feature extraction, and model optimization.
Section 4- What is meant by matrix
Def: A matrix is a rectangular array of numbers written between square brackets.
Def : A matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. It is often denoted by a capital letter.
Def: In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. A matrix could be reduced as a submatrix of a matrix by deleting any collection of rows and/or columns.
Matrices provide a convenient way to represent and manipulate data in various fields such as physics, computer science, economics, and more.
There are a number of basic operations that can be applied to modify matrices:
Addition
Scalar Multiplication
Transposition
Multiplication.
Section 5- Matrix example
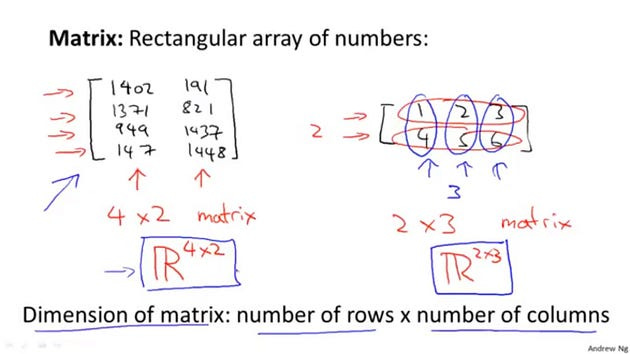
So, for example, here is a matrix on the right, a left square bracket. And then, write in a bunch of numbers. These could be features from a learning problem or it could be data from somewhere else, but the specific values don’t matter, and then I’m going to close it with another right bracket on the right. And so that’s one matrix. And, here’s another example of the matrix, let’s write 3, 4, 5,6. So matrix is just another way for saying, is a 2D or a two dimensional array.
Section 6- Dimension of the matrix
And the other piece of knowledge that we need is that the dimension of the matrix is going to be written as the number of row times the number of columns in the matrix. So, concretely, this example on the left, this has 1, 2, 3, 4 rows and has 2 columns, and so this example on the left is a 4 by 2 matrix — number of rows by number of columns. So, four rows, two columns. This one on the right, this matrix has two rows. That’s the first row, that’s the second row, and it has three columns. That’s the first column, that’s the second column, that’s the third column So, this second matrix we say it is a 2 by 3 matrix. So we say that the dimension of this matrix is 2 by 3. Sometimes you also see this written out, in the case of left, you will see this written out as R4 by 2 or concretely what people will sometimes say this matrix is an element of the set R 4 by 2. So, this thing here, this just means the set of all matrices that of dimension 4 by 2 and this thing on the right, sometimes this is written out as a matrix that is an R 2 by 3. So if you ever see, 2 by 3. So if you ever see something like this are 4 by 2 or are 2 by 3, people are just referring to matrices of a specific dimension.
Section 7- How to refer to specific elements of the matrix
Next, let’s talk about how to refer to specific elements of the matrix. And by matrix elements, other than the matrix I just mean the entries, so the numbers inside the matrix. So, in the standard notation, if A is this matrix here, then A sub-strip IJ is going to refer to the i, j entry, meaning the entry in the matrix in the ith row and jth column. So for example a1–1 is going to refer to the entry in the 1st row and the 1st column, so that’s the first row and the first column and so a1–1 is going to be equal to 1, 4, 0, 2. Another example, 8 1 2 is going to refer to the entry in the first row and the second column and so A 1 2 is going to be equal to one nine one. This come from a quick examples. Let’s see, A, oh let’s say A 3 2, is going to refer to the entry in the 3rd row, and second column, right, because that’s 3 2 so that’s equal to 1 4 3 7. And finally, 8 4 1 is going to refer to this one right, fourth row, first column is equal to 1 4 7 and if, hopefully you won’t, but if you were to write and say well this A 4 3, well, that refers to the fourth row, and the third column that, you know, this matrix has no third column so this is undefined, you know, or you can think of this as an error. There’s no such element as 8 4 3, so, you know, you shouldn’t be referring to 8 4 3. So, the matrix gets you a way of letting you quickly organize, index and access lots of data. In case I seem to be tossing up a lot of concepts, a lot of new notations very rapidly, you don’t need to memorize all of this,
Section 8- Vectors
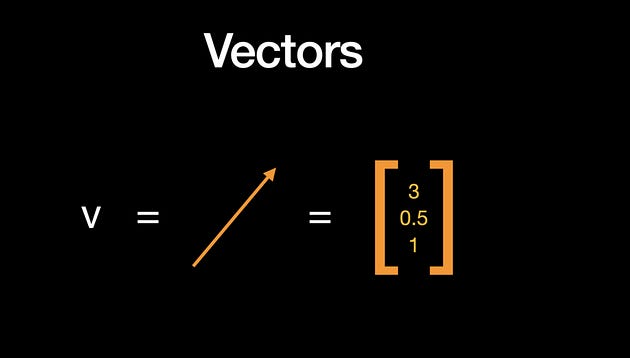
A vector is an ordered collection of elements or quantities represented as a column or row matrix. It is often denoted by a lowercase letter or boldface letter. Vectors have both magnitude and direction.
Vector Notation
Vectors can be represented using angle brackets or parentheses enclosing their components. For example, consider the following vector v:
v = [v1]
[v2]
[v3]
Here, v1, v2, etc., represent the components or elements of the vector.
Vector is “The range that connects the origin of the space t0 point P“. A vector is quantified by its Magnitude and direction. Magnitude is given by sum of the squares of co-ordinates and then take square root of it. Direction is based on the values of Co-ordinates, can be left/right of origin and similarly up/down of origin.
Next, let’s talk about what is a vector. A vector turns out to be a special case of a matrix. A vector is a matrix that has only 1 column so you have an N x 1 matrix, then that’s a remember, right? N is the number of rows, and 1 here is the number of columns, so, so matrix with just one column is what we call a vector.
So here’s an example of a vector, with I guess I have N equals four elements here. so we also call this thing, another term for this is a four dmensional vector, just means that this is a vector with four elements, with four numbers in it. And, just as earlier for matrices you saw this notation R3 by 2 to refer to 2 by 3 matrices, for this vector we are going to refer to this as a vector in the set R4. So this R4 means a set of four-dimensional vectors.
Section 9- How to refer to specific elements of the Vector
Next let’s talk about how to refer to the elements of the vector. We are going to use the notation yi to refer to the ith element of the vector y. So if y is this vector, y subscript i is the ith element. So y1 is the first element,four sixty, y2 is equal to the second element, two thirty two -there’s the first. There’s the second. Y3 is equal to 315 and so on, and only y1 through y4 are defined consistency 4-dimensional vector. Also it turns out that there are actually 2 conventions for how to index into a vector and here they are. Sometimes, people will use one index and sometimes zero index factors. So this example on the left is a one in that specter where the element we write is y1, y2, y3, y4. And this example in the right is an example of a zero index factor where we start the indexing of the elements from zero. So the elements go from a zero up to y three. And this is a bit like the arrays of some primary languages where the arrays can either be indexed starting from one. The first element of an array is sometimes a Y1, this is sequence notation I guess, and sometimes it’s zero index depending on what programming language you use. So it turns out that in most of math, the one index version is more common For a lot of machine learning applications, zero index vectors gives us a more convenient notation. So what you should usually do is, unless otherwised specified, you should assume we are using one index vectors. In fact, throughout the rest of these videos on linear algebra review, I will be using one index vectors. But just be aware that when we are talking about machine learning applications, sometimes I will explicitly say when we need to switch to, when we need to use the zero index vectors as well. Finally, by convention, usually when writing matrices and vectors, most people will use upper case to refer to matrices. So we’re going to use capital letters like A, B, C, you know, X, to refer to matrices, and usually we’ll use lowercase, like a, b, x, y, to refer to either numbers, or just raw numbers or scalars or to vectors. This isn’t always true but this is the more common notation where we use lower case “Y” for referring to vector and we usually use upper case to refer to a matrix. So, you now know what are matrices and vectors. Next, we’ll talk about some of the things you can do with them
Section 10- Types of Vectors
Row Vector: A row vector has only one row and multiple columns. For example:
u = [u1 u2 u3]
Column Vector: A column vector has only one column and multiple rows. For example:
w = [w1]
[w2]
[w3]
Section 10- Matrix in Python
Matrix or Array of Arrays
import numpy as np # The swiss knife of the data scientist.
alist = [1, 2, 3, 4, 5] # Define a python list. It looks like an np array
narray = np.array([1, 2, 3, 4]) # Define a numpy array
npmatrix1 = np.array([narray, narray, narray]) # Matrix initialized with NumPy arrays
npmatrix2 = np.array([alist, alist, alist]) # Matrix initialized with lists
npmatrix3 = np.array([narray, [1, 1, 1, 1], narray]) # Matrix initialized with both types
print(npmatrix1)
print(npmatrix2)
print(npmatrix3)
okmatrix = np.array([[1, 2], [3, 4]]) # Define a 2x2 matrix
print(okmatrix) # Print okmatrix
print(okmatrix * 2) # Print a scaled version of okmatrixConclusion
Matrices and vectors are foundational concepts in linear algebra that enable us to solve complex systems of equations, perform transformations, and understand higher-dimensional spaces. Understanding these concepts is crucial for various fields ranging from computer science to physics and economics. By grasping the properties, operations, and applications of matrices and vectors, we gain powerful tools for analysis and problem-solving in diverse domains.
Please Subscribe 👏Course teach for Indepth study of Machine Learning
🚀 Elevate Your Data Skills with Coursesteach! 🚀
Ready to dive into Python, Machine Learning, Data Science, Statistics, Linear Algebra, Computer Vision, and Research? Coursesteach has you covered!
🔍 Python, 🤖 ML, 📊 Stats, ➕ Linear Algebra, 👁️🗨️ Computer Vision, 🔬 Research — all in one place!
Don’t Miss Out on This Exclusive Opportunity to Enhance Your Skill Set! Enroll Today 🌟 at
Understanding of Machine Learning Course!
Artificial Intelligence Career Advice Course
Stay tuned for our upcoming articles because we research end to end , where we will explore specific topics related to Machine Learning in more detail!
🔍 Explore Tools, Python libraries for ML, Slides, Source Code, Free Machine Learning Courses from Top Universities and More!
Remember, learning is a continuous process. So keep learning and keep creating and Sharing with others!💻✌️
Note:if you are a Machine Learning export and have some good suggestions to improve this blog to share, you write comments and contribute.
if you need more update about Machine Learning and want to contribute then following and enroll in following
👉Course: Machine Learning (ML)
We offer following serveries:
We offer the following options:
Enroll in my ML course: You can sign up for the course at this link. The course is designed in a blog-style format and progresses from basic to advanced levels.
Access free resources: I will provide you with learning materials, and you can begin studying independently. You are also welcome to contribute to our community — this option is completely free.
Online tutoring: If you’d prefer personalized guidance, I offer online tutoring sessions, covering everything from basic to advanced topics. please contact:mushtaqmsit@gmail.com
Contribution: We would love your help in making coursesteach community even better! If you want to contribute in some courses , or if you have any suggestions for improvement in any coursesteach content, feel free to contact and follow.
Together, let’s make this the best AI learning Community! 🚀
Source
1- Machine Learning — Andrew
2-How Machine Learning Uses Linear Algebra to Solve Data Problems
5–Linear Algebra that every Machine Learning Engineer should know