📚Chapter 3: Sentiment Analysis (Naive Bayes)
If you want to read more articles about NLP, don’t forget to stay tuned :) click here.
Sections
Conditional probabilities
Bayes Rules
Section1- Conditional probabilities
We will be looking at conditional probabilities to help us understand Bayes rule. In other words, if I tell you, you can guess what the weather is like given that we are in California and it is winter, then you’ll have a much better guess than if I just asked you to guess what the weather is like. In order to derive Bayes rule, let’s first take a look at the conditional probabilities.
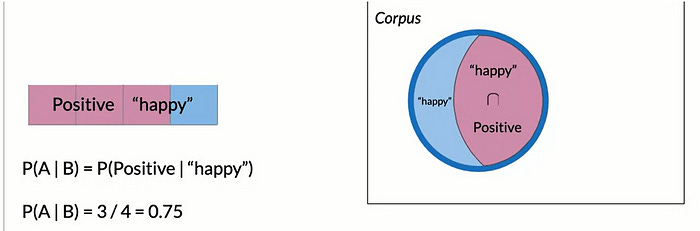
Now think about what happens if, instead of the entire corpus, you only consider tweets that contain the word happy. This is the same as saying, given that a tweet contains the word happy with that, you would be considering only the tweets inside the blue circle, where many of the positive tweets are now excluded. In this case, the probability that a tweet is positive, given that it contains the word happy, simply becomes the number of tweets that are positive and also contain the word happy. We divide that by the number that contains the word happy. As you can see by this calculation, your tweet has a 75 percent likelihood of being positive if it contains the word happy.
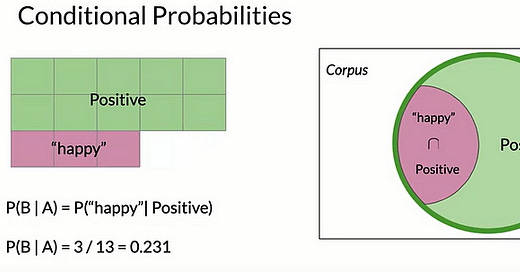
You could make the same case for positive tweets. The purple area denotes the probability that a positive tweet contains the word happy. In this case, the probability is 3 over 13, which is 0.231.
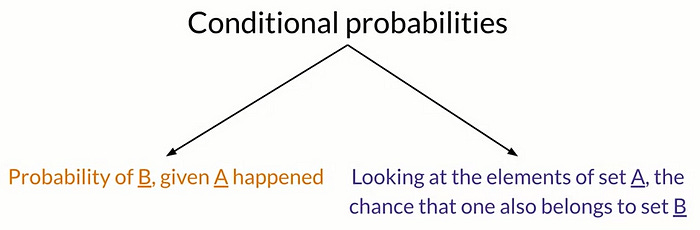
With all of this discussion of the probability of missing certain conditions, we are talking about conditional probabilities. Conditional probabilities could be interpreted as the probability of an outcome B knowing that event A already happened, or given that I’m looking at an element from set A, the probability that it’s also belongs to set B.
Here’s another way of looking at this with a Venn diagram you saw before. Using the previous example, the probability of a tweet being positive, given that it has the word happy, is equal to the probability of the intersection between the tweets that are positive and the tweets that have the word happy divided by the probability of a tweet given from the corpus having the word happy.
Section 2- Bayes Rules
Let’s take a closer look at the equation from the previous slide. You could write a similar equation by simply swapping the position of the two conditions. Now, you have the conditional probability of a tweet containing the word happy, given that it is a positive tweet. Armed with both of these equations, you’re now ready to derive Bayes rule.
To combine these equations, note that the intersection represents the same quantity, no matter which way it’s written. Knowing that, you can remove it from the equation, with a little algebraic manipulation, you are able to arriveat this equation.
This is now an expression of Bayes rule in the context of the previous sentiment analysis problem. More generally, Bayes rule states that the probability of x given y is equal to the probability of y given x times the ratio of the probability of x over the probability of y. That’s it. You just arrived at the basic formulation of
Bayes rule, nicely done.
To wrap up, you just derive Bayes rule from expressions of conditional probability. Throughout the rest of this course, you’ll be using Bayes rule for various applications in NLP. The main takeaway for now is that, Bayes rule is based on the mathematical formulation of conditional probabilities. That’s with Bayes rule, you can calculate the probability of x given y if you already know the probability of y given x and the ratio of the probabilities of x and y. That’s great work. I’ll see you later. Congratulations. You now have a good understanding of Bayes rule. In the next video, you’ll see how you can start applying Bayes rule to a model known as Naive Bayes. This will allow you to start building your sentiment analysis classifier using just probabilities.
Takeaway
You’ve now seen how Bayes’ Rule emerges naturally from conditional probabilities.
Bayes' Rule allows us to invert probabilities and use prior knowledge to update beliefs based on new evidence — a cornerstone in building models like Naive Bayes classifiers for tasks such as sentiment analysis.
Stay tuned for our next lesson, where we’ll apply this to build an actual Naive Bayes model for NLP!
🚀 Want to Learn More?
📌 Follow Coursesteach for updates on machine learning, NLP, data science, and more!
💬 Are you an NLP expert with ideas to improve this blog? Drop your comments — we love contributions!
🔗 Resources and Community
👉 Course: Natural Language Processing (NLP)
📝 Notebook
💬 Need help getting into Data Science and AI?
I offer research supervision and career mentoring:
📧 Email: mushtaqmsit@gmail.com
💻 Skype: themushtaq48