Introduction to Neural Networks: How They Extend Logistic Regression

DL(Part 18)

📚Chapter4: Shallow Neural Network

If you want to read more articles about Deep Learning, don’t forget to stay tuned :) click here.

Introduction

Understanding neural networks begins with building on the foundation of logistic regression. This blog dives into the core concepts of neural networks, their computation process, and the essential notations used to differentiate layers and training examples. By the end, you’ll see how a neural network is essentially an extension of logistic regression, performed multiple times, with forward and backward propagation at its heart.

Sections

What is Neural Network
Recap: Logistic Regression
Transition to Neural Networks
Computation in Neural Networks
Introducing Notation for Layers
Differentiating Training Examples and Layers
Forward Propagation Steps
Neural Networks as Logistic Regression Repeated
Backward Propagation in Neural Networks
Summary of Neural Networks
What’s Next?

Section 1- What is Neural Network

A neural network is a layered structure of interconnected nodes (also called neurons), where each node processes and passes information to the next layer. These connections are weighted, much like biological synapses. Each neuron:

1. Takes input from the previous layer

2. Computes a weighted sum plus a bias

3. Applies an activation function

4. Passes the result to the next layer

Think of it as a series of simple calculations, repeated over many layers

Def: A neural network consists of layers of interconnected called, which process transmit information through weighted connections known synapses. Each neuron receives input from the in the preceding, applies an activation function to the sum its inputs, and then passes the output to the next layer

But for now, let’s give a quick overview of how you implement a neural network.

Section 2- Recap: Logistic Regression

Before we jump into neural networks, let’s revisit logistic regression, a fundamental building block in deep learning.

In logistic regression:

• You compute a linear combination of inputs: z = w·x + b

• Apply the sigmoid function: a = sigmoid(z)

• The output a (or ŷ) represents the probability of a class label

This setup is quite similar to what we do inside a single node of a neural network.

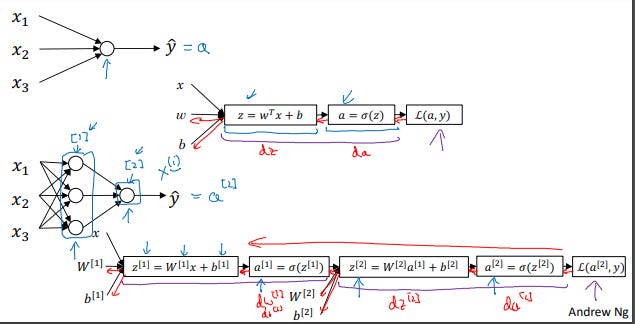
Last week, we had talked about logistic regression, and we saw how this model corresponds to the following computation draft, where you then put the features x and parameters w and b that allows you to compute z which is then used to computes a, and we were using a interchangeably with this output y hat and then you can compute the loss function.

Section 3- Transition to Neural Networks

A neural network is basically logistic regression... repeated multiple times.

Where logistic regression performs a single z → a step, neural networks stack many of these steps together. Each additional layer helps capture more complex patterns in the data.

A neural network looks like this. As I’d already previously alluded, you can form a neural network by stacking together a lot of little sigmoid units. Whereas previously, this node corresponds to two steps of calculations:

1. Compute the z-value.

2. Compute the a-value.

Section 4- Computation in Neural Networks

In this neural network, this stack of nodes will correspond to a z-like calculation like this, as well as an a-like calculation like that. Then, that node will correspond to another z and another a-like calculation.

Let’s break down what’s happening in a simple neural network:

• The first layer performs:
  z₁ = w₁·x + b₁
a₁ = sigmoid(z₁)

• The second layer continues with:
  z₂ = w₂·a₁ + b₂
a₂ = sigmoid(z₂)

The final output, a₂, serves as the network's prediction (ŷ).

Section 5- Introducing Notation for Layers

The notation which we will introduce later will look like this:

• First, we’ll input the features, x, together with some parameters w and b, and this will allow you to compute z1.

• New notation that we’ll introduce is that we’ll use superscript square bracket [1] to refer to quantities associated with this stack of nodes, it’s called a layer.

• Later, we’ll use superscript square bracket [2] to refer to quantities associated with that node. That’s called another layer of the neural network.

The superscript square brackets, like we have here, are not to be confused with the superscript round brackets which we use to refer to individual training examples.

To keep things organized, we use different notations:

• Square brackets for layers:
  z[1], a[1] → layer 1
  z[2], a[2] → layer 2

• Round brackets for training examples:
  x(i) → the i-th training example

So a refers to the output of the second layer for the third training example.

Section 6-Differentiating Training Examples and Layers

Whereas x(i) refers to the i-th training example, superscript square brackets [1] and [2] refer to these different layers — layer 1 and layer 2 in this neural network.

It’s easy to get confused between layer numbers and example indices. Just remember:

• [1], [2] refer to layers

• (i) refers to a specific example

So z[1] is layer 1’s computation, while x(1) is the first example in your training set.

Section 7-Forward Propagation Steps

But so going on, after computing z_1 similar to logistic regression, there’ll be a computation to compute a_1, and that’s just sigmoid of z_1, and then you compute z_2 using another linear equation and then compute a_2. A_2 is the final output of the neural network and will also be used interchangeably with y-hat.

Here’s how forward propagation works in a 2-layer neural network:

1. Compute z[1] = w[1]·x + b[1]

2. Compute a[1] = sigmoid(z[1])

3. Compute z[2] = w[2]·a[1] + b[2]

4. Compute a[2] = sigmoid(z[2]) → this is the final prediction ŷ

Each layer follows the same logic: linear combination → activation.

Section 7- Neural Networks as Logistic Regression Repeated

So, I know that was a lot of details, but the key intuition to take away is that whereas for logistic regression, we had this z followed by an a-calculation, in this neural network, here we just do it multiple times:

• z-calculation.

• a-calculation.

• Finally, compute the loss at the end.

This is the core idea:

A neural network is just logistic regression applied multiple times — layer after layer.

Every layer does a:

• Linear computation (z)

• Activation (a)

• Followed by the next layer’s computation

Section 8-Backward Propagation in Neural Networks

You remember that for logistic regression, we had this backward calculation in order to compute derivatives or as you’re computing your d a, d z and so on. So, in the same way, a neural network will end up doing a backward calculation that looks like this in which you end up computing da_2, dz_2, that allows you to compute dw_2, db_2, and so on. This right to left backward calculation that is denoting with the red arrows.

Just like logistic regression has gradient computations, neural networks use backward propagation to compute gradients for all layers.

Starting from the last layer, we calculate:

• da[2], dz[2], dw[2], db[2]

• Then move to: da[1], dz[1], dw[1], db[1]

These gradients help update the weights during training using methods like gradient descent.

Section 9-Summary of Neural Networks

So, that gives you a quick overview of what a neural network looks like. It’s basically taken logistic regression and repeating it twice.

Section 10-What’s Next?

I know there was a lot of new notation laws, new details, don’t worry about saving them, follow everything, we’ll go into the details most probably in the next few blog. So, let’s go on to the next blog. We’ll start to talk about the neural network representation.

Here’s a simple way to think about it:

• Neural networks are multiple logistic regressions stacked together

• Forward propagation moves inputs through the layers

• Backward propagation calculates how to adjust weights

• Notation helps keep track of layers and training examples

🎯 Call to Action

Liked this tutorial?
👉 Subscribe to our newsletter for more Python + ML tutorials
👉 Follow our GitHub for code notebooks and projects
👉 Leave a comment below if you’d like a tutorial on vectorized backpropagation next!

👉, Improve Neural network: Enroll for Full Course to find notes, repository etc.

👉, Deep learning and Neural network: Enroll for Full Course to find notes, repository etc.

🎁 Access exclusive Deep learning bundles and premium guides on our Gumroad store: From sentiment analysis notebooks to fine-tuning transformers—download, learn, and implement faster.

Source

1- Neural Networks and Deep Learning