Explaining Gradient Descent in Logistic Regression: How It Works and Its Impact on Model Performance

DL(Part 8)

📚Chapter2: Logistic Regression as a Neural Network

If you want to read more articles about Deep Learning, don’t forget to stay tuned :) click here.

Sections

Introduction
Understanding the logistic regression
Introduction of Gradient Descent
What is a gradient, and how is it used in a gradient descent algorithm?
Why Is Gradient Descent Necessary for Machine Learning?
How the Gradient Descent Algorithm Works
More details about gradient Descent
Advantages of Gradient Descent in Logistic Regression
Limitations of Gradient Descent in Logistic Regression
Basic implementation of Logistic Regression Gradient in Python
Conclusion

1- Introduction

Logistic regression is a popular machine learning algorithm used for binary classification problems. It is widely used in various domains such as finance, healthcare, and marketing. One of the key components of logistic regression is gradient descent, which is an optimization algorithm used to find the optimal parameters of the model. In this blog post, we will delve into the concept of gradient descent in logistic regression, exploring its workings, advantages, and limitations.

You’ve seen the logistic regression model, and you’ve seen the loss function that measures how well you’re doing on the single training example. You’ve also seen the cost function that measures how well your parameters W and B are doing on your entire training set.

2. Understanding Logistic Regression

Before diving into gradient descent, it’s essential to understand the basics of logistic regression. Logistic regression is a statistical model that predicts the probability of a binary outcome based on one or more independent variables. It uses a logistic function (also known as the sigmoid function) to map the output between 0 and 1, representing the probability of the positive class. The goal of logistic regression is to find the best-fitting line (or hyperplane) that separates the two classes.

2- Optimization algorithms

Optimizers are methods or algorithms designed to tweak a model’s attributes, like weights and learning rate, to reduce the error or loss function while training a machine learning model. The main objective of an optimizer is to find the optimal set of parameters that result in the best performance of the model on the given dataset. There are many type of optimization algorithm which show below

Gradient Descent,Stochastic Gradient Descent, Momentum + SGD, Nesterov Accelerated Gradient,Adagrad,RMSprop,Adadelta,Adafactor,Follow-the-Regularized-Leader,Adam,AdamW,Adamax,Nadam,Lion

3- Introduction of Gradient Descent

It’s a powerful tool used to optimize the parameters of a model and minimize its error or cost function [2].In simple terms, gradient descent is a process of finding the minimum point of a function by following the steepest descent direction [2]. Gradient descent is an iterative optimization algorithm that is widely used in machine learning. At a high level, gradient descent is a method for finding the minimum value of a function by iteratively adjusting the function’s parameters based on the gradient (i.e., the direction of the steepest descent) [2].

Gradient descent is an optimization algorithm used to minimize the cost function (also known as the loss function) in machine learning models. In logistic regression, the cost function is based on the difference between the predicted probabilities and the actual labels. The aim is to minimize this difference and find the best parameters that maximize the model’s accuracy.

By using gradient descent to minimize the cost function of a machine learning model, we can find the best set of model parameters for accurate predictions. This means that it helps us find the best values for our model’s parameters so that our model can make accurate predictions [2].

It’s used in a wide range of machine-learning algorithms, Such as [2]

• Linear regression,

• Logistic regression,

• Neural networks.

4- What is a gradient, and how is it used in a gradient descent algorithm?

A gradient is a derivative of a function with more than one input variable in machine learning. In other words, it assesses how sensitive a function’s output is to input changes [2].This information is critical for the gradient descent algorithm, which uses the gradient to update the parameters in the opposite direction of the gradient towards the cost function’s minimum point [2].

The gradient points toward the steepest ascent, so we simply negate the gradient vector to find the direction of the steepest descent. The gradient vector’s magnitude tells us the cost function’s slope in that direction, which is useful for determining the step size of the gradient descent algorithm [2].

If the slope is steep, we take a larger step toward the minimum point, and if the slope is shallow, we take a smaller step to avoid overshooting the minimum point [2].

It is worth noting that the gradient from X0 to X1 is substantially longer than the one from X3 to X4. This is due to a decrease in the steepness/slope of the hill, which defines the length of the vector.

This precisely illustrates the hill example since the hill becomes less steep as one climbs higher. As a result, a lower gradient corresponds to a lower slope and a smaller step size for the hill climber.

5- Why Is Gradient Descent Necessary for Machine Learning?

Gradient descent is necessary for optimizing and fine-tuning the parameters of a machine-learning model. In fact, it is the backbone of many machine-learning algorithms. Gradient descent aims to minimize a model’s cost or loss function, which measures how well the model performs [2].

By reducing the cost function, the model becomes better at making predictions and can generalize better to new data. The gradient descent process involves iteratively adjusting the model parameters based on the gradient of the cost function [2].

This means that the model moves toward the steepest descent toward the minimum point of the cost function. With gradient descent, finding the optimal set of parameters for a given model would be much easier, and the model’s performance would improve as a result [2].

6- How the Gradient Descent Algorithm Works

Now let’s talk about how you can use the gradient descent algorithm to train or to learn the parameters W on your training set. To recap here (Figure 1) is the familiar logistic regression algorithm and we have on the second line the cost function J, which is a function of your parameters W and B. And that’s defined as the average is one over m times has some of this loss function.

Figure 1

Loss or Cost function: And so the loss function measures how well your algorithms outputs Y hat I on each of the training examples stacks up compares to the ground true labels Y (it) on each of the training examples. The full formula is expanded out on the right [1].

A cost function (also known as a loss function) in machine learning is a function that evaluates the difference between the expected and actual output. A cost function, in other terms, is a mathematical function that measures how well your model fits your data [2]. The learning algorithm aims to minimize this cost function, representing how well the model performs on training data [2]. First, we define an objective function, typically represented as f(x), that we want to minimize. In machine learning, the loss or cost function often measures the difference between the model’s predictions and the actual target values.

So the cost function measures how well your parameters w and b are doing on the training set. So in order to learn a set of parameters w and b, it seems natural that we want to find w and b. That make the cost function J of w, b as small as possible.

So, The Figure 1 show an illustration of gradient descent. In this diagram, the horizontal axes represent your space of parameters w and b in practice w can be much higher dimensional, but for the purposes of plotting, let’s illustrate w as a singular number and b as a singular number. The cost function J of w, b is then some surface above these horizontal axes w and b. So the height of the surface represents the value of J, b at a certain point. And what we want to do really is to find the value of w and b that corresponds to the minimum of the cost function J.

Convex and Non-Convex Function: It turns out that this particular cost function J is a convex function. So it’s just a single big bowl, so this is a convex function and this is as opposed to functions that look like this, which are nonconvex and have lots of different local optimal. So the fact that our cost function J of w, b as defined here is convex, is one of the huge reasons why we use this particular cost function J for logistic regression.

It’s important to remember that gradient descent can converge to a local minimum instead of a global minimum, especially when the cost function is non-convex. Various techniques, such as using different initialization values or optimizing the learning rate, can help overcome this issue [2].

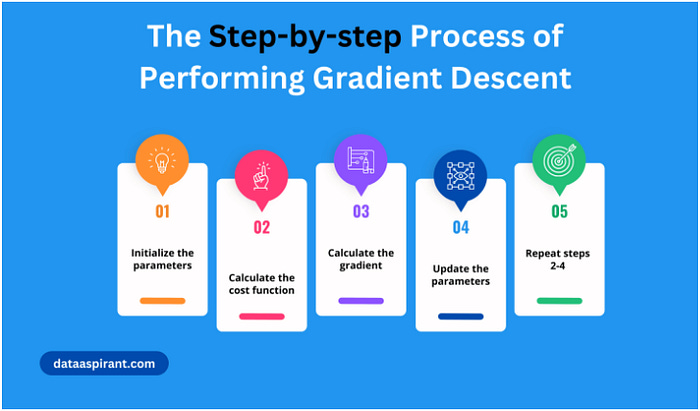
7- The Steps of performing gradient Descent

Initialize the parameters:

So to find a good value for the parameters, what we’ll do is initialize w and b to some initial value may be denoted by that little red dot. And for logistic regression, almost any initialization method works. Usually, you Initialize the values of 0. Random initialization also works, but people don’t usually do that for logistic regression. But because this function is convex, no matter where you initialize, you should get to the same point or roughly the same point.

And what gradient descent does is it starts at that initial point and then takes a step in the steepest downhill direction. So after one step of gradient descent, you might end up there because it’s trying to take a step downhill in the direction of steepest descent or as quickly down who as possible. So that’s one iteration of gradient descent. And after iterations of gradient descent, you might stop there, three iterations and so on. I guess this is not hidden by the back of the plot until eventually, hopefully you converge to this global optimum or get to something close to the global optimum. So this picture illustrates the gradient descent algorithm.

8- More details about gradient Descent

Figure 2

Let’s write a little bit more of the details for the purpose of illustration in Figrue 2, let’s say that there’s some function J of w that you want to minimize and maybe that function looks like this to make this easier to draw. I’m going to ignore b for now just to make this one-dimensional plot instead of a higher-dimensional plot. So gradient descent does this. We’re going to repeatedly carry out the following update.

We’ll take the value of w and update it. Going to use colon equals to represent updating w. So set w to w minus alpha times and this is a derivative d of J w d w. And we repeatedly do that until the algorithm converges.

Learning rate: So a couple of points in the notation alpha here is the learning rate and controls how big a step we take on each iteration are gradient descent [1], The learning rate is a hyperparameter that determines how big of steps we take along our cost function while trying to reach its minimum value. In other words, it controls how much the parameters are adjusted in the direction of the negative gradient. The learning rate is a critical parameter that can significantly impact the convergence and accuracy of the model [2]. If the learning rate is too small, the algorithm takes small steps toward the minimum point, which can lead to slow convergence and the possibility of getting stuck in a local minimum. On the other hand, if the learning rate is too large, the algorithm takes large steps toward the minimum point, which can cause overshooting and oscillation around the minimum point. Therefore, choosing an appropriate learning rate is crucial for the success of the gradient descent algorithm. Typically, the learning rate is determined through trial and error or using optimization techniques such as grid search or random search [2]. The learning rate controls how aggressively the algorithm moves towards the minimum, with smaller values leading to slower convergence and larger values potentially causing overshooting or instability [2].

Derivative:- here in Figure 2, this is a derivative. This is basically the update of the change you want to make to the parameters w, when we start to write code to implement gradient descent, we’re going to use the convention that the variable name in our code, d w will be used to represent this derivative term. So when you write code, you write something like w equals or cold equals w minus alpha time’s d w. So we use d w to be the variable name to represent this derivative term. Now, let’s just make sure that this gradient descent update makes sense. Let’s say that w was over here. So you’re at this point on the cost function J of w. Remember that the definition of a derivative is the slope of a function at the point. So the slope of the function is really, the height divided by the width right of the lower triangle.

Gradient calculation- The gradient of the function, ∇f(x), is a vector that points in the direction of the steepest increase of the function at point x. It’s calculated by taking the partial derivatives of the function with respect to each variable (i.e., the model’s parameters). The gradient gives us the direction we should move in to minimize the function [2]. Here, in Figure 2 this tension to J of w at that point. And so here the derivative is positive. W gets updated as w minus a learning rate times the derivative, the derivative is positive. And so you end up subtracting from w. So you end up taking a step to the left and so gradient descent with, make your algorithm slowly decrease the parameter.

To perform the gradient descent, we iteratively update the variables (parameters) according to the following rule:

x_new = x_old — α * ∇f(x_old)

Here,

• x_old represents the current values of the variables,

• α is the learning rate (a hyperparameter that determines the step size of each update),

• x_new are the updated values of the variables

If you had started off with this large value of w. As another example, if w was over here, then at this point the slope here or dJ detail, you will be negative. And so they driven to send update with subtract alpha times a negative number. And so end up slowly increasing w. So you end up you’re making w bigger and bigger with successive generations of gradient descent. So that hopefully whether you initialize on the left, wonder right, create into central move you towards this global minimum here.

Repeat steps- But the overall intuition for now is that this term represents the slope of the function and we want to know the slope of the function at the current setting of the parameters so that we can take these steps of steepest descent so that we know what direction to step in in order to go downhill on the cost function J. So we wrote our gradient descent for J of w. If only w was your parameter in logistic regression. Your cost function is a function above w and b. In that case the inner loop of gradient descent, that is this thing here the thing you have to repeat becomes as follows. You end up updating w as w minus the learning rate times the derivative of J of wb respect to w and you update b as b minus the learning rate times the derivative of the cost function respect to b. So these two equations at the bottom of the actual update you implement as in the side,

Partial derivative:- this symbol (Figure 2), this is actually just the lower case d in a fancy font, in a stylized font. But when you see this expression, all this means is this is the of J of w, b or really the slope of the function J of w, b how much that function slopes in the w direction. And the rule of the notation and calculus, which I think is in total logical. But the rule in the notation for calculus, which I think just makes things much more complicated than you need to be is that if J is a function of two or more variables, then instead of using lower case d. You use this funny symbol. This is called a partial derivative symbol, but don’t worry about this. And if J is a function of only one variable, then you use lower case d. So the only difference between whether you use this funny partial derivative symbol or lowercase d. As we did on top is whether J is a function of two or more variables. In which case use this symbol, the partial derivative symbol or J is only a function of one variable. Then you use lower case d. This is one of those funny rules of notation and calculus that I think just make things more complicated than they need to be. But if you see this partial derivative symbol, all it means is you’re measuring the slope of the function with respect to one of the variables, and similarly to adhere to the, formally correct mathematical notation calculus because here J has two inputs. Not just one. This thing on the bottom should be written with this partial derivative simple, but it really means the same thing as, almost the same thing as lowercase d. Finally, when you implement this in code, we’re going to use the convention that this quantity really the amount I wish you update w will denote as the variable d w in your code. And this quantity, right, the amount by which you want to update b with the note by the variable db in your code. All right. So that’s how you can implement gradient descent.

9. Advantages of Gradient Descent in Logistic Regression

Gradient descent offers several advantages when used in logistic regression:

Flexibility: Gradient descent can be applied to various optimization problems beyond logistic regression.
Efficiency: It allows us to efficiently optimize complex models with a large number of parameters.
Convergence: With careful tuning of hyperparameters, gradient descent can converge to an optimal solution.
Scalability: By using mini-batch or stochastic gradient descent, it can handle large datasets efficiently.

10. Limitations of Gradient Descent in Logistic Regression

While gradient descent is a powerful optimization algorithm, it has certain limitations:

Local Minima: Gradient descent can get stuck in local minima instead of reaching the global minimum.
Sensitivity to Initial Parameters: The choice of initial parameters can affect convergence and model performance.
Learning Rate Selection: Selecting an appropriate learning rate can be challenging and may require experimentation.
Feature Scaling: Gradient descent can be sensitive to feature scaling, requiring preprocessing techniques like normalization or standardization.

11- Basic implementation of Logistic Regression Gradient in Python

1-Import the necessary libraries.

import numpy as np 
import pandas as pd

2- Load the training data.

data = pd.read_csv("train.csv")

3- Split the data into features and target.

X = data.drop("target", axis=1) 
y = data["target"]

4- Initialize the model parameters.

theta = np.random.randn(X.shape[1])

5- Define the sigmoid function.

def sigmoid(z):
 return 1 / (1 + np.exp(-z))

6- Define the loss function.

def loss(theta, X, y):
 h = sigmoid(X.dot(theta)) 
return -np.sum(y * np.log(h) + (1 - y) * np.log(1 - h))

7-Define the gradient descent algorithm.

def gradient_descent(theta, X, y, alpha, num_iterations): 
    for i in range(num_iterations):
        h = sigmoid(X.dot(theta)) 
        gradient = X.T.dot(y - h) 
        theta -= alpha * gradient 
return theta

8- Train the model.

theta = gradient_descent(theta, X, y, alpha=0.01, num_iterations=1000)

9- Make predictions.

def predict(theta, X): 
    h = sigmoid(X.dot(theta)) 
    y_pred = np.where(h >= 0.5, 1, 0) 
   return y_pred

y_pred = predict(theta, X)

10-Evaluate the model.

accuracy = np.mean(y_pred == y) 
print("Accuracy:", accuracy)

Conclusion

Gradient descent plays a vital role in optimizing logistic regression models by iteratively updating the parameters in the direction of steepest descent. It offers flexibility, efficiency, and scalability while providing solutions to binary classification problems. However, it is important to be aware of its limitations and consider techniques like feature scaling and careful selection of hyperparameters for optimal performance.

Please Follow and 👏 Clap for the story courses teach to see latest updates on this story

🚀 Elevate Your Data Skills with Coursesteach! 🚀

Ready to dive into Python, Machine Learning, Data Science, Statistics, Linear Algebra, Computer Vision, and Research? Coursesteach has you covered!

🔍 Python, 🤖 ML, 📊 Stats, ➕ Linear Algebra, 👁️‍🗨️ Computer Vision, 🔬 Research — all in one place!

Join the full course for More Learning!🌟

Neural Networks and Deep Learning course

Improving Deep Neural Network course

Stay tuned for our upcoming articles because we reach end to end ,where we will explore specific topics related to Deep Learning in more detail!

📚GitHub Repository

We offer following serveries:
We offer the following options:

1. Enroll in my Deep Learning course: You can sign up for the course at this link. The course is designed in a blog-style format and progresses from basic to advanced levels.

2. Access free resources: I will provide you with learning materials, and you can begin studying independently. You are also welcome to contribute to our community — this option is completely free.

3. Online tutoring: If you’d prefer personalized guidance, I offer online tutoring sessions, covering everything from basic to advanced topics.

Contribution: We would love your help in making coursesteach community even better! If you want to contribute in some courses , or if you have any suggestions for improvement in any coursesteach content, feel free to contact and follow.

Together, let’s make this the best AI learning Community! 🚀

👉WhatsApp

👉 Facebook

👉Github

👉LinkedIn

👉Youtube

👉Twitter

References

1- Neural Networks and Deep Learning

2– HOW THE GRADIENT DESCENT ALGORITHM WORKS

3-Enhancing Multi-Layer Perceptron Performance: Demystifying Optimizers